In the previous post of the series, I considered a simplificated relation between contact patch area, vertical load and tire pressure to be able to calculate sinkage depth and relationate it with Crr. This relation considered that the pressure was constant over the contact patch but, as pressure peaks around the center of the contact patch and is zero in its limits, I was underestimating the area of the contact patch and, consequently, the sinkage depth for a given combination of normal load and tire pressure. This underestimation modified the relation between sinkage depth and Crr
In this new approach, I won't rely on contact patch surface to calculate sinkage depth. I will rather use wheel's vertical stiffness. The vertical stiffness of a tire is a product of air pressure principally because shoulder stiffness is very low. The relation between vertical stiffness and inflating pressure is sigmoidal but linear over typical values of pressure. Knowing that a road tire inflated up to 100psi has a vertical stiffness of 150000 N/m, we can calculate vertical stiffness for any pressure and determinate sinkage depth for a given load. After checking the results of the previous approach, I noticed that the sinkage depths were a bit too small. With this new method, the sinkage depths are 60-80% higher and they seem more plausible. This new approach gives the following relation between sinkage depth and Crr for the Specialized Turbo 25c clincher tire:
 |
| As you can see, the shape is still linear but the coefficients have changed |
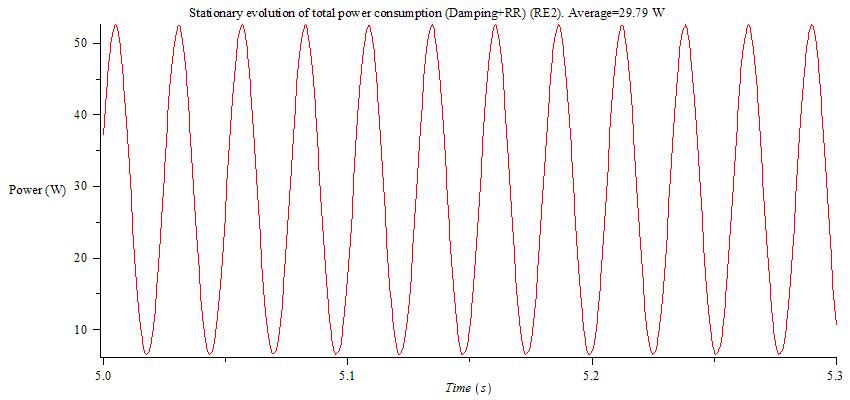
For this new relation, total power consumption in tire-ground contact for both rear ends showed in the previous post are the following ones:
Absolute value have changed but still 3.4W higher power consumption by increasing chainstay's diameter by just 8mm
Additionally, the flexibility of this new approach have allowed me to determinate the contact patch pressure function for an uncambered toroidal wheel. The shape of the pressure function proposed depends on the author of the paper that you read but it's typically considered to be unidimensional and sometimes doesn't consider the shift of the center of pressure caused by rolling resistance or it is said to change of shape depending on the slip. As Cossalter presented in one of his books and some FEA studies have endorsed, I'm inclined to think that the vertical pressure distribution is constant independently of the slip. Taking this into account, I propose the following bidimensional pressure distribution for a toroidal wheel:
 |
| R and r are the two defining radius of the torus. sk is the sinkage depth. a and b are two tuning parameters. x is the travelling direction. y is the perpendicular direction in the contact patch |
This function assures that the pressure is null in the limits of the contact patch and allows the shift of the center of pressure to translate the rolling resistance. The tuning parameters a and b are negative and their modules increase when the sinkage depth is decreased. The innovation of this approach is the obtention of these coefficients using experimental data of Crr (something similar could be done for the overturning moment). As the center of pressure is independent of the slip, the relation that says that Crr is the ratio between the shift of the center of pressure and the rolling radius for a wheel turning at constant angular speed is applicable. Knowing this, we can calculate the shift of the center of pressure for every inflating pressure (that modifies vertical stiffness and, consequently, sinkage depth) for a given load. The two equations that allow me to calculate both coefficients are 1) the integral of the pressure distribution over the contact patch is equal to the vertical load and 2) the center of pressure in the travelling direction is equal to the product of tire's external radius minus sinkage depth and Crr. This system of equations involves integrals over a complex area and can't be computed analitically. I have solved it for every pressure using a Mathematica+MAPLE combo (Mathematica to compute the integrals and MAPLE to solve the system numerically) because none of the programs could solve the whole problem. Some graphical representations of the pressure distribution:
 |
| R=0.3275m. r=0.0125m. sk=0.002556m. Pressure=127.91psi. Load=490.5N. Stiffness=191862.2N/m. Crr=0.004081 Contact patch for the previous conditions |
 |
| Same conditions. Cut for y=0 to show the displacement of the center of pressure that translates the rolling resistance |
 |
| R=0.3275m. r=0.0125m. sk=0.006544m. Pressure=49.97psi. Load=490.5N. Stiffness=74952.98N/m. Crr=0.007098 |
Contact patch for the previous conditions
That's all for today. Thanks for reading!
PD If you analyze the pressure distributions, you will see that the average pressure in the contact patch is approximately equal to the inflating pressure. There is an interesting relation between contact pressure, sinkage depth, Crr, inflating pressure and tire stiffness.